Solving An Absolute Value Inequality

The absolute number of a number a is written as

$$\left | a \correct |$$

And represents the distance between a and 0 on a number line.

An accented value equation is an equation that contains an absolute value expression. The equation

$$\left | x \right |=a$$

Has two solutions x = a and 10 = -a considering both numbers are at the altitude a from 0.

To solve an absolute value equation as

$$\left | ten+seven \correct |=xiv$$

You brainstorm by making information technology into ii separate equations and then solving them separately.

$$10+7 =xiv$$

$$x+7\, {\color{green} {-\, seven}}\, =fourteen\, {\color{greenish} {-\, 7}}$$

$$x=7$$

$$ten+7 =-14$$

$$ten+7\, {\color{green} {-\, 7}}\, =-14\, {\color{green} {-\, 7}}$$

$$x=-21$$

An absolute value equation has no solution if the absolute value expression equals a negative number since an absolute value tin never exist negative.

The inequality

$$\left | x \correct |<2$$

Represents the distance betwixt 10 and 0 that is less than 2

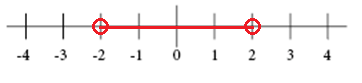
Whereas the inequality

$$\left | x \right |>two$$

Represents the altitude between ten and 0 that is greater than 2

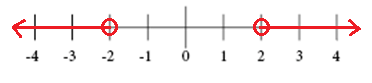
You tin can write an absolute value inequality as a compound inequality.

$$\left | x \correct |<two\: or

$$-2<x<two$$

This holds true for all absolute value inequalities.

$$\left | ax+b \right |<c,\: where\: c>0$$

$$=-c<ax+b<c$$

$$\left | ax+b \right |>c,\: where\: c>0$$

$$=ax+b<-c\: or\: ax+b>c$$

You can replace > above with ≥ and < with ≤.

When solving an absolute value inequality it's necessary to start isolate the accented value expression on i side of the inequality before solving the inequality.

Case

Solve the accented value inequality

$$2\left |3x+9 \right |<36$$

$$\frac{2\left |3x+9 \right |}{two}<\frac{36}{two}$$

$$\left | 3x+nine \right |<18$$

$$-18<3x+ix<xviii$$

$$-18\, {\colour{light-green} {-\, 9}}<3x+nine\, {\color{dark-green} {-\, 9}}<18\, {\color{green} {-\, 9}}$$

$$-27<3x<9$$

$$\frac{-27}{{\color{green} 3}}<\frac{3x}{{\color{green} 3}}<\frac{9}{{\color{green} 3}}$$

$$-9<10<three$$